DCF-77 und Fehlerkorrektur

Diese Seite beschreibt Überlegungen zur Implementierung eines DCF-Empängers in Software. Falls Du noch nicht mit dem Aufbau des DCF-Signals vertraut bist, findest Du Erklärungen und hilfreiche Texte auf den folgenden Seiten:

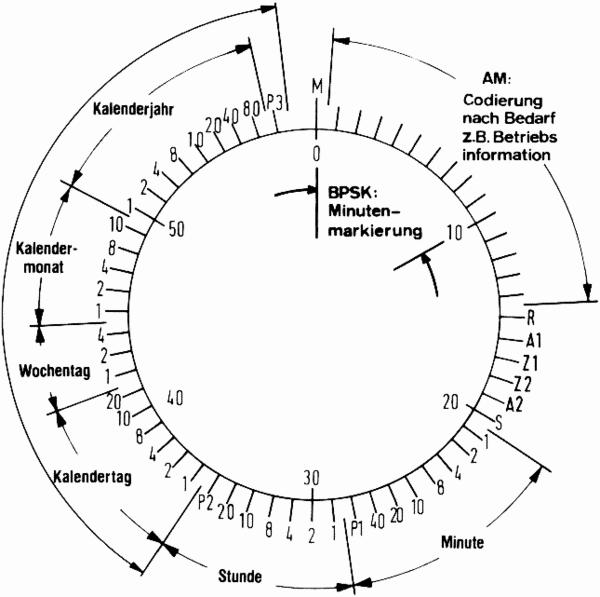
Das deutsche Funkuhr-Signal DCF77 wird amplitudenmoduliert mit einer Trägerfrequenz von 77.5 kHz von Mainflingen bei Franfurt/Main ausgestrahlt. Die Übertragungsrate beträgt ein Bit pro Sekunde.

Durch Absenkung des Trägers für 100ms zum Sekundenanfang wird eine Null — im folgenden mit B₀ bezeichnet — übertragen. Analog wird eine Eins, also B₁, durch eine Absenkung von 200ms Dauer codiert. Auf diese Weise werden jede Minute 59 Bit übermittelt, die unter anderem die Zeitinformation für die folgende Minute im BCD-Format enthalten. In der 60-ten Sekunde wird der Träger nicht abgesenkt, bezeichnet als B_M oder #. Die Marke B_M dient als Kennung der Minutenenden, das heißt mit dem Ende von B_M und dem Anfang des nächsten Bits beginnt die Minute, deren Zeitinformation soeben übertragen wurde.

Zu diesen drei Werten kommt aus Sicht eines Empfängers noch ein vierter Wert hinzu: B_?. Er steht für einen nicht zuortenbaren Wert, der bei schlechter Empfangslage auftreten kann.

Strategie

Die Strategie eines einfachen DCF-Decoders ist simpel: Es werden solange Bits empfangen bis eine Minute komplett ist. Dann werden die Daten decodiert. Weicht ein Bit weiter als eine vorgegebene Maximaltoleranz vom DCF-Format ab, dann beginnt man einfach von vorne mit dem Einsammeln der Bits.

Mit dieser Strategie dauert ein Zeitabgleich bei guter Empfangslage nur wenige Minuten; ist das Signal jedoch gestört, dann ist ein Zeitabgleich sehr unwahrscheinlich: Gehen wir davon aus, dass zur Dekodierung 65 Bits in Folge korrekt empfangen werden müssen und die Wahrscheinlichkeit für ein korrekt empfangenes Bit bei 90% liegt, dann liefert ein naives Wahrscheinlichkeitsmodell eine zu erwartende Zeit von rund 16 Stunden (0.9⁻⁶⁵ Minuten), bis ein Abgleich erfolgreich ist. Sollen sogar zwei Minuten in Folge fehlerfrei empfangen werden, um die Daten der beiden Minuten gegeneinander zu testen, dann erhöht sich die erwartete Zeit auf ein Jahr, nämlich auf 0.9⁻¹²⁵ Minuten.

Die Wahrscheinlichkeit, dass bei zwei aufeinander folgenden Minuten ein bestimmtes Bit nicht empfangen wurde liegt bei 1−0.9·0.9 = 1%. Könnten wir nichtbekannte Bits von der vorherigen Minute übernehmen, ergäbe sich eine Wahrscheinlichkeit von 0.99⁶⁵ ≈ 0.52 dafür, dass wir alle Bits zusammen haben. Sollen zwei aufeinander folgende dieser 2-Minuten-Einheiten für einen Integritätstest verwendet werden, dann brauch man 4 dieser 2-Minuten-Einheiten. Die Empfangsdauer von einem Jahr reduziert sich daher mit der Fehlerkorrektur auf rund 10 Minuten.

Auch wenn das Wahrscheinlichkeitsmodell stark vereinfacht — Übertragungsfehler sind unabhängig voneinander und es besteht Minuten-Synchronität — zeigt die Betrachtung das Potential einer Fehlerkorrektur.

Die Probleme einer Fehlerkorrektur sind erhöhter Resourcen-Bedarf an Daten- und Programmspeicher, Laufzeit, Hirnschmalz und Entwicklungszeit. Hinzu kommt die Möglichkeit der Fehlerausbreitung bei Kuckuksei-Bits. Daher müssen sämtliche Möglichkeiten der Fehler-Erkennung genutzt werden, um die Wahrscheinlichkeit falsch empfangener Daten zu minimieren, das heißt praktisch auszuschließen.

Zur Fehler-Erkennung und -Vermeidung bieten sich viele naheliegende Wege, die im folgenden Abschnitt kurz und kommentarlos zusammengefasst werden.

Fehler-Vermeidung

Die Empfangsbedingungen können das Signal abschwächen/stören und damit zu Bitfehlern oder nicht zu identifizierten Bits B_? beitragen.

Monitore und Rechner
Schaltnetzteile etc.
Metallteile und Stahlbeton
mangelhafte Antennenausrichtung
zu große Toleranzen für die Bitlängen in der Software

In simpler DCF-Software werden üblicherweise Intervalle für die Bitlängen implementiert, zum Beispiel 90ms–110ms für B₀. Bei schlechter Empfangslage ist es nicht ratsam, diese Toleranz – welche im übrigen schon eine Art der Fehlerkorrektur darstellt – zu groß zu wählen. Das ist zwar verlockend, weil die Längen der Signale bei schlechtem Empfang in weiteren Grenzen variieren, es erhöht aber die Wahrscheinlichkeit von Bitfehlern. Es ist wesentlich unkritischer, für ein Bit den Wert B_? einzutragen, als schwer erkennbare Bitfehler zu riskieren.

Im allgemeinen kann gesagt werden, dass bei schlechtem Empfang die Bitlängen kleiner erscheinen als vom Sender ausgesandt, was wohl auf atmosphärische Störungen zurückzuführen ist. Durch die Störung wird auch bei abgesenktem Signal etwas empfangen. Daher wird öfter fälschlicherweise B₀ anstatt B₁ erkannt als umgekehrt. Analog wird öfter B_M anstatt B₀ erkannt als umgekehrt.

Erschwerend kommt hinzu, dass viele DCF-Empfänger einen AGC (Automatic Gain Control) zum Pegelangleich an die Signalstärke besitzen, der das Signal ebenvalls verziehen kann.

Fehler-Erkennung

Bit-Integrität

Der Abstand (in einer noch festzulegenden Metrik) zu einem der Bits B₀, B₁, B_M ist hinreichend klein

Protokoll-Integrität

Die Minuten-Marken sind im richtigen Abstand
Bit 0 ist Null und Bit 20 ist Eins
Zwei aufeinanderfolgende Minuten sind nie beide gerade oder beide ungerade

Daten-Integrität

Die empfangenen Zeitwerte für Minute, Stunde, etc sind im BCD-Format
Die Zeitwerte liegen in den erlaubten Bereichen; die Minuten zum Beispiel im Intervall von 0 bis 59
Die Paritätsprüfung ist OK
Es ist nicht gleichzeitig Sommer- und Winterzeit
Es gibt keinen Widerspruch zu den Daten der vorhergehenden Minute(n)/Decodierung(en)

Synchronisation

Sekunden-Sync

Bei verrauschtem Signal variieren sowohl die Sekunden-Anfänge als auch ihre Längen. Zudem gibt es hin und wieder Spikes auf dem Signal. Daher kann es mit einem klassischen Empfänger schwierig sein, den Sekundenanfang zu detektieren und auch bei Störungen nachzuverfolgen.

Als praktikabel erweist sich die Berechnung der zyklischen Faltung mittels Haar-Wavelets wie in der Animation rechts verdeutlicht. Zunächst sei angemerkt, dass die Faltungen auch mit begrenzten Resourcen, wie sie typischerweise auf Mikrocontrollern vorherrschen, gut berechnet werden können.

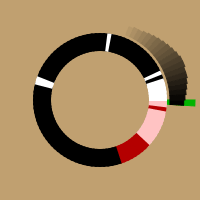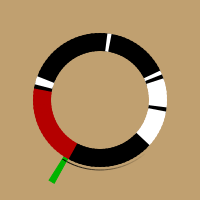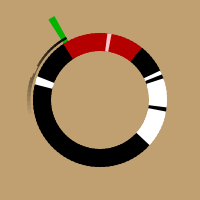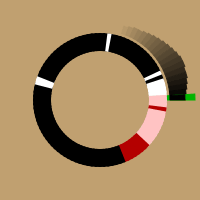
Im Bild ist ein schwarz-weißer Kreisring zu sehen, der eine Sekunde darstellt und aus 100 Stücken besteht; jedes Stückchen stellt einen Zeitraum von 10ms dar und ist eingefärbt anhand des vom DCF-Empfänger abgefragten Wertes: Weiß für abgesenkten Träger und Schwarz für vollen Träger. Rechts im Bild wurde wohl für 200ms (1/5 des Kreises) der Träger abgesenkt, was einem B₁ entspricht. Hinzu kommen einige Spikes.

Rot unterlegt ist ein 200ms breites Haar-Wavelet, mit dem gefaltet wird. Werden pro Sekunde N Samples abgefragt und hat das Wavelet die Breite w, werden für j = 0..N−1 die Summen

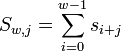
     $S_{w,j} = \sum_{i=0}^{w-1} s_{i+j}$

berechnet. Indizes sind dabei immer modulo N zu nehmen. In der Animation ist dieser Wert in Grün unterlegt. Ist ein Wert berechnet, können die Folgewerte effizient über die Beziehung

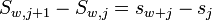
     $S_{w,j+1} - S_{w,j}= s_{w+j} -s_j$

erhalten werden. Damit sind nicht mehr N·w Schleifendurchläufe pro Sekunde und Wavelet nötig, sondern lediglich N+w. Außerdem müssen die Werte nicht gespeichert werden; es genügt, das Maximum und dessen Position zu kennen:

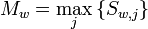
     $M_w = \max_j \{S_{w,j}\}$

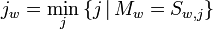
     $j_w = \min_j \{j | M_w = S_{w,j}\}$

Bis zur Sekunden-Synchronisation werden diese Faltungen berechnet. Wird ein Bit als B₀ oder B₁ kategorisiert, dann geht es in die Berechnung des Sekunden-Anfanges ein. Hierzu werden alle Samples der "guten" Sekunden aufsummiert – im Endeffekt also gemittelt – und nach einigen Sekunden die Faltungen über diese Summen berechnet. Liegen Positionen der Maxima für M_100ms und M_200ms hinreichend dicht zusammen, dann ist dies der Anfang der Sekunde.

Nach erfolgtem Sekunden-Abgleich gehen die guten Bits weiterhin in die Bestimmung des Sekunden-Anfanges ein. Zur Unterscheidung, ob es sich bei einem empfangenen Wert um B₀, B₁, B_M oder B_? handelt, muss nur noch an der Position des Sekunden-Anfangs gefaltet werden. Der Sekunden-Anfang muss ständig nachgeregelt werden, weil er sich durch Änderung der Empfangslage etwas verschieben kann und durch Ungenauigkeit der internen Zeitbasis (i.d.R ein Schwingquarz) wegzulaufen scheint.

Minuten-Sync

Fehlerkorrektur

Das Zeitsignal besteht aus mehreren Ziffern, welche alle binär übertragen werden. Von einer Minute zur nächsten gibt es drei Möglichkeiten, wie sich eine solche Ziffer ändern kann:

Die Ziffer bleibt unvervändert
Die Ziffer wird um Eins erhöht
Die Ziffer wird von ihrem Maximalwert auf ihren Minimalwert zurückgesetzt (Reset)

Ziffern in diesem Sinne sind zum Beispiel:

Einer der Minute/Stunde (min=0, max=9)
Zehner der Minute/Stunde (min=0, max=5)
Wochentag (min=1, max=7)

Die Minute selbst ist nicht als Ziffer anzusehen, weil es von Minute 9 zu Minute 10 aufgrund der BCD-Codierung eine Erhöhung des Wertes von 9 auf 16 (9₁₆ auf 10₁₆) gibt; ähnliches gilt für Stunde, Tag, Monat, und Jahr.

Kann ein Reset der Ziffer ausgeschlossen werden, dann ergeben sich aus den Übergängen eines ihrer Bits folgende Schlussfolgerungen, denn eine Ziffer wird maximal um 1 erhöht:

0→0: alle höherwertigen Bits bleiben unverändert
0→1: alle höherwertigen Bits bleiben unverändert
1→1: alle höherwertigen Bits bleiben unverändert

Dabei ist die Wertigkeit der Parity-Bits von der Größenordnung wie das LSB der Werte, für die es codiert. Das Minuten-Parity hat also die Wertigkeit von Bit Minute.0.

Hieran ist folgendes zu erkennen:

Fehlerkorrektur ist auf Bit-Ebene möglich, und Fehler pflanzen sich mit dieser Methode nicht auf benachbarte Bits fort.
Die Fehlerkorrektur sollte nach Möglichkeit bei den niederwertigsten Bits beginnen. Kann aufgrund der Werte eine Fehlerkorrektur erst später – etwa beim Monat – beginnen, können nicht mehr viele Bits korrigiert werden. Daher werden zur Entscheidung, ob eine Fehlerkorrektur möglich ist, nur die Minuten-Bits verwendet. Höhere Bits in die Entscheidung einzubeziehen bringt mehr Aufwand, jedoch kaum weiteren Gewinn.
Reset-Wert von Minuten-Einer und -Zehner ist 0; wird also eine 1 in den Minuten-Bits empfangen, dann gab es von der vorhergehenden auf die aktuelle Minute keinen Reset, daher können dann alle höheren Bits korrigiert werden.

Ein besonders einfacher Spezialfall sind die ungeraden Minuten, d.h. Minuten, für die gilt Minute.0 = 1. Dieser Fall ist sehr einfach zu testen und liegt jede zweite Minute vor: Alle höherwertigen Bits dürfen kopiert werden. Das Minuten-Parity muss wechseln. Der Wechsel von Minute.0 geschieht in jeder Minute, unabhängig von Sommer- und Winterzeit und von Schaltjahren und -sekunden. Der Wechsel von Minute.0 kann sogar zur Minuten-Synchronisation verwendet werden, weil kein anderes Bit diese Eigenschaft hat, und daher sind sogar Bitfehler in Minute.0 erkennbar bzw. selbst wenn Minute.0 als B_? empfangen wurde, ist dessen Wert bekannt. Die Fehlerkorrektur beruht in diesem Fall also auch nie auf einer falschen Grundlage wie zum Beispiel einem Fehlerbit (einer 0/1-Verwechslung).

Fehlerkorrektur: Ein Beispiel

Unten folgen zwei Bilder der fehlerkorriegerte Daten des schwarz-weissen Spaghetti-Bildes links. Jeder Pixel des linken Bildes stellt 10ms dar: Abgesekter Träger ist in Weiß codiert, nicht-abgesenkter Träger in Schwarz. Jede Zeile repräsentiert eine Sekunde empfangener Daten und ist somit 100 Pixel breit. Die Gesamtdauer des Streifens ist 14231 Sekunden, also knapp 4 Stunden.

Du kannst die PNG-Datei verwenden, um Deinen eigenen Fehler-Korrektur-Ansatz zu testen. Speichere dazu das Bild auf Deinem Rechner und wandle es mit einem Grafik-Progamm in das PBM-Format um. Das geht zum Beipiel mit convert:

   convert -compress None dcf-10ms-pulses.png dcf-10ms-pulses.pbm

Das erzeugt die PBM-Datei, also einfachen Text. Die Datei sieht so aus (Schwarz=1 und Weiß=0), und damit kannst Du Dein Programm füttern:

   P1
   100 14231
   1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
   1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0
   0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
   ...

Folgende Bilder zeigen fehlerkorrigierte DCF-Daten. Jede Zeile enthält eine Minute, also 60 farbcodierte Sekunden:

Schwarz	B₀	Null
Weiß	B₁	Eins
Blau	B_M	Minutenmarke
Grün	B_?	Unbekannt
Rot	B₀ ↔ B₁	Ein Kuckucksei: B₀ statt B₁ oder umgekehrt korrigiert zu B_?
Braun	B₁	Beginn der Zeitinfo

Im linken Bildteil sind die Originaldaten, rechts die Daten nach Fehlerkorrektur. Die Blöcke sind getrennt durch einen hallblau hinterlegten Streifen von 3 Paritätsbits für Minute, Stunde und Datum, welche sich auf den rechten, fehlerkorrigierten Block beziehen.

Grün	B₀	Parity OK
Gelb	B_?	Parity unbekannt
Rot	B₁	Parity fehlerhaft

Zeilen mit 3 grünen Parity-Bits können also weiterverarbeitet werden, indem zum Beispiel weitere Konsistenztest zur Datenintegrität folgen. Daten-Tests 1) bis 3) von oben wurden in den Bildern schon durchgeführt, Daten-Tests 4) und 5) noch nicht.

Verfahren: Z-Parity (Z₀): Hier wird als Grundlage nur Bit 0 der Minute verwendet. In geraden Minuten geschieht keine Fehlerkorrektur oder -erkennung. In den ungeraden Minuten können unbekannte Bits aus der vorherigen, geraden Minute übernommen werden bzw. die Bits der beiden Minuten gegeneinander getestet werden: alle Bits ab Minute.1 müssen gleich geblieben sein, und das Minuten-Parity muss wechseln. Es kann also auch geprüft werden, ob das Minuten-Parity richtig übertragen wurde!

Fehlerkorrigierte DCF-Daten, Bit 21

Anmerkung:: Die blaue Minuten-Marke im linken Block zeigt nicht die Empfangslage, sondern ergibt sich aus der Minuten-Synchronisation. Auch der Beginn der Zeit-Information (Bit 20 in Braun und Bit 21) im rechten Teilbild wurden so erhalten und sind deshalb selbst bei stark gestörtem Signal bekannt.

Verfahren: Z_0–6: Hier dienen alle Bits der Minute als Entscheidungsgrundlage: Falls ein Bit der momentanen Minute vom Minimalwert 0 abweicht, oder ein Bit der vorhergehenden Minute vom Maximalwert 59₁₆ abweicht, dann muss für alle höherwertigen Bits dieser beiden Minuten Gleichheit herrschen. Wie man sieht, gibt es hier deutlich mehr brauchbare Daten. Im unteren Bildteil gibt es viele komplett nutzbare Datensätze – erkennbar an einem zu der Minute gehörenden grünen Mittelbalken – und es wurden mehr Übertragungsfehler erkannt und korrigiert.

Bei Stundenwechseln ist eine Fehlerkorrektur aufgrund des Minuten-Resets nicht mehr möglich; es können also keine Bits aus der Vorminute übernommen werden. Daher dauert es einige Zeit, bis wieder alle Bits aufgesammelt sind und die Zeitinformation komplett ist.

Fehlerkorrigierte DCF-Daten, Bits 21-27